作者:老余捞鱼
原创不易,转载请标明出处及原作者。

写在前面的话:在这篇文章中,我将带你深入探索外汇市场的统计套利策略。通过分析顶级对冲基金的操作和实用的Python代码示例(附完整可运行代码),我将展示如何在货币对间寻找盈利机会,并探讨策略的风险管理。让我们一起来挖掘这个外汇市场中的隐秘金矿,开启稳定盈利之路。
一、发现外汇交易中的统计套利
有没有想过对冲基金是如何不受市场走向影响而赚钱的?让我揭示他们的秘密武器之一:统计套利。这不是简单的“低买高卖”,而是一种挖掘大多数交易者未曾察觉的一种数学策略。
什么是配对交易统计套利策略?
配对交易统计套利是一种基于统计学原理的交易策略,旨在利用相关资产之间的价格差异进行获利。该策略通常涉及选择一对高度相关的金融工具(如股票、ETF或外汇等资产),并在它们的价格关系偏离历史均衡时进行交易。这种方法的核心在于,随着时间的推移,价格关系会回归到其历史平均水平,从而为交易者提供获利机会。
配对交易的基本原理是利用两种资产之间的价格关系。例如,当A资产的价格上涨而B资产的价格未能同步上涨时,交易者可能会卖空A资产并买入B资产,期待价格关系最终回归正常。
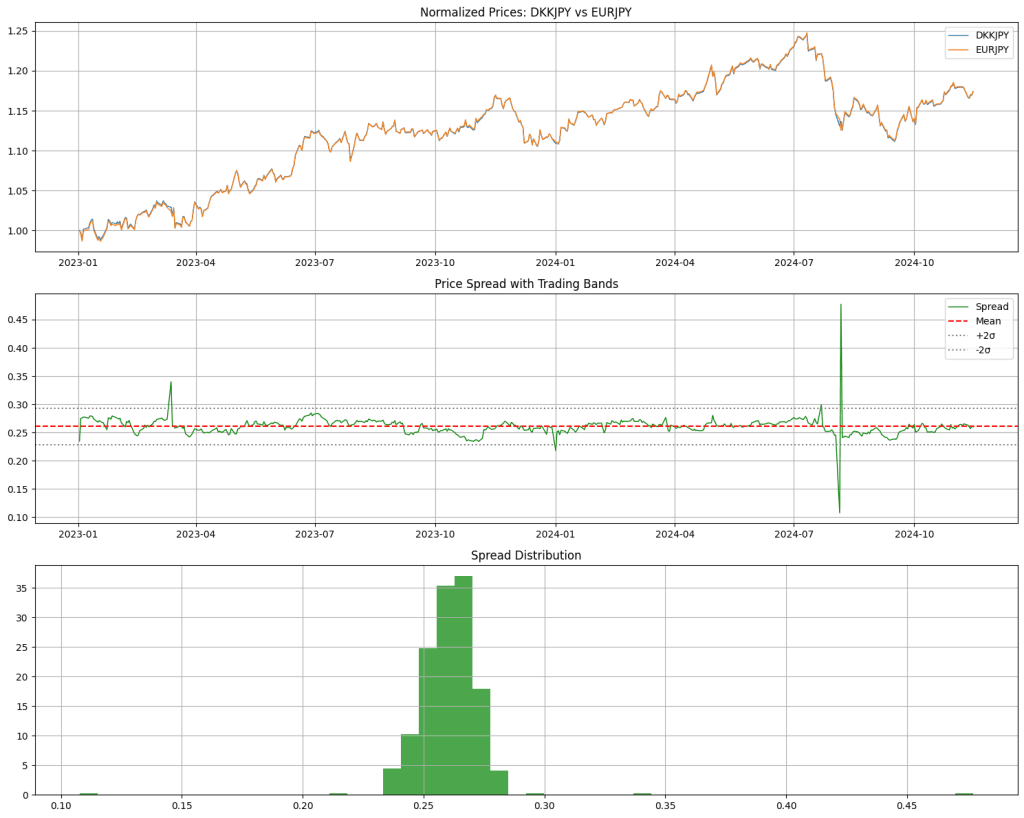
在分析外汇市场交易数据时,我偶然发现了一个现象:有些货币对的走势就像天平两端的砝码一样。以 DKK&JPY(丹麦克朗对日元)和 EUR&JPY(欧元对日元)为例,它们之间的关系有严谨的数学表达。接下来让我们来分析一下发现这些数字:
# The magic numbers
P-Value: 0.0001 (99.99% confidence!)
Hedge Ratio: 0.1325
Half-Life: 0.7 days首先,让我们来看看我们是如何找到这些”黄金“配对的:
def test_cointegration(pair1, pair2, data, significance_level=0.05):
try:
# Calculate the optimal hedge ratio
Y = data[pair1].values
X = data[pair2].values
X = np.vstack([X, np.ones(len(X))]).T
beta = np.linalg.lstsq(X, Y, rcond=None)[0][0]
# Find the spread
spread = data[pair1] - beta * data[pair2]
# Test for cointegration
result = adfuller(spread.dropna())
p_value = result[1]
# Calculate mean reversion speed
spread_lag = spread.shift(1)
spread_diff = spread - spread_lag
model = np.polyfit(spread_lag.dropna(), spread_diff.dropna(), 1)
half_life = -np.log(2) / model[0] if model[0] < 0 else np.inf
return (p_value < significance_level, p_value, beta, half_life)
except Exception as e:
return (False, 1.0, 0, np.inf)步骤 1:查找关系
beta = np.linalg.lstsq(X, Y, rcond=None)[0][0]划出这条线可以找到货币对之间的完美比例。
步骤 2:测试强度
result = adfuller(spread.dropna())
p_value = result[1]这就好比测试桥梁的强度。我们的 p 值为 0.0001,说明这座桥是由钛合金制成的。
步骤 3:测量速度
# Calculate half-life of mean reversion
spread_lag = spread.shift(1) #Calculate the Lagged Spread
spread_diff = spread - spread_lag #Calculate the Difference in Spread
spread_lag = spread_lag.dropna() # ignoring any NaN values
spread_diff = spread_diff.dropna()
# This fits a linear model to the lagged spread and the spread difference
model = np.polyfit(spread_lag, spread_diff, 1)
# This calculates the half-life based on the slope of the linear model
half_life = -np.log(2) / model[0] if model[0] < 0 else np.inf这就告诉我们,我们的配对在分离后重新聚在一起的速度有多快。0.7 天意味着它们就像磁铁一样,不会分开太久!
二、交易策略
2.1 策略实现
现在,令人兴奋的地方来了……当 DKKJPY 和 EURJPY 出现分歧时,我们:
- 购买一对(如 DKK&JPY)。
- 以我们的神奇对冲比率卖出另一个(EUR&JPY)。
- 等待他们重归于好。
- 实现盈利!
下面是代码实现部分:
position_size = 10000 # Base position in DKKJPY
hedge_amount = position_size * 0.1325 # Amount of EURJPY to short
# Entry conditions
spread = dkkjpy_price - (0.1325 * eurjpy_price)
spread_mean = spread.rolling(window=20).mean()
spread_std = spread.rolling(window=20).std()
# Entry signals
if spread > spread_mean + (2 * spread_std):
# Short DKKJPY, Long EURJPY
print("Short DKKJPY, Long EURJPY")
elif spread < spread_mean - (2 * spread_std):
# Long DKKJPY, Short EURJPY
print("Long DKKJPY, Short EURJPY")2.2 风险控制
- 货币挂钩:丹麦克朗是与欧元挂钩的,但这种挂钩关系如果发生脱钩呢?需要关注。
- 交易成本:半衰期为 0.7 天,您需要频繁交易。
- 杠杆作用:需要小心的控制上杠杆的系数。
2.3 实现步骤
配对交易的总体实时步骤如下图:

而在我们这个实战环境中,在原则不变的情况下,请按下面的步骤执行:
- 设置 Python 环境;
- 下载最新外汇数据;
- 进行协整检验;
- 监测不同资产之间的价差(如下表中的各种外汇对);
- 建议回测后,从小资金量交易开始。
GBPNOK USDHKD 0.0008 -13.3588 16.2
EURGBP USDHKD 0.0009 0.4942 12.2
EURNZD GBPAUD 0.0010 0.5560 10.5
CADJPY NOKJPY 0.0017 7.7633 15.1
SGDJPY ZARJPY 0.0018 11.6076 15.1为了帮助您入门,我在 Google Colab 上分享了本文中使用的代码。请仔细研究、调整,并将其变成你自己的代码!地址:https://colab.research.google.com/drive/1EhSrkss-m83RHLVlhBXT2bADwPGCQnwY?usp=sharing
三、观点总结
统计套利就像是在数据河中寻找小金块。它需要耐心、精确和一点点数学公式的魔法。但是一旦你做对了……盈利的可能性就是无穷的!
- 统计套利是一种利用数学和统计方法在外汇市场中寻找盈利机会的策略。
- 货币对之间的协整关系是统计套利策略的基础,可以通过计算P-值和对冲比例来验证。
- 均值回归速度,即价差的半衰期,是评估交易机会的关键指标。
- 交易策略应包括明确的入场和出场条件,以及对风险的管理。
- 实施统计套利策略时需要注意交易成本、货币政策变化和杠杆作用的风险。
- 持续的学习和适应市场变化是成功应用统计套利策略的关键。
请记住市场总是在不断变化,因此要不断测试和调整你的策略。最重要的是,永远不要停止学习!
感谢您阅读到最后,希望本文能给您带来新的收获。祝您投资顺利!如果对文中的内容有任何疑问,请给我留言,必复。
本文内容仅限技术探讨和学习,不构成任何投资建议。
Be First to Comment