
写在前面的话:汤普森抽样是一种在不确定性环境下做决策的核心方法,以威廉·汤普森(William R. Thompson)命名,是一种启发式策略,用于解决多臂强盗问题中的探索与开发的困境。在强盗游戏中,你只有两种可能的结果:赢或输。汤普森抽样的主要步骤包括选择与随机产生的信念相关的预期奖励最大的行动,并利用过去的结果来更新对未来哪些行动最有价值的信念。对于股票交易者来说,这意味着他们需要根据各种股票的表现来调整他们的投资策略。
在错综复杂的股市投资中,每一步都至关重要。Thompson Sampling 基于贝叶斯概率,为我们提供了一种复杂而直观的方法,使这些决策变得有意义。这一切都是为了从过去的经验中汲取教训,以便在现在做出更明智的选择,特别是在购买、持有或出售股票时。了解贝塔分布(Beta Distribution)对于理解汤普森抽样的原理至关重要。贝塔分布是一组定义在区间 [0,1] 上的连续概率分布,通常用于描述事件的概率密度分布。它有两个参数,其中一个参数表示事件的成功次数,另一个参数表示失败次数。贝塔分布的概率密度函数如下:

其中,B(α, β) 是贝塔函数,而 α 和 β 分别是贝塔分布的参数。这个分布在机器学习和数理统计学中有广泛应用。
现在,我们来看看汤普森抽样的应用。汤普森抽样是一种用于在不断试错的过程中学习并在探索和利用之间取得平衡的策略。它通过随机抽样来估计每个动作的潜在回报,并选择具有最高抽样值的动作。贝塔分布在这里起到了关键作用,因为它可以描述每个动作的概率分布。所以,了解贝塔分布有助于我们理解汤普森抽样的基本原理,从而更好地应用于其他领域。
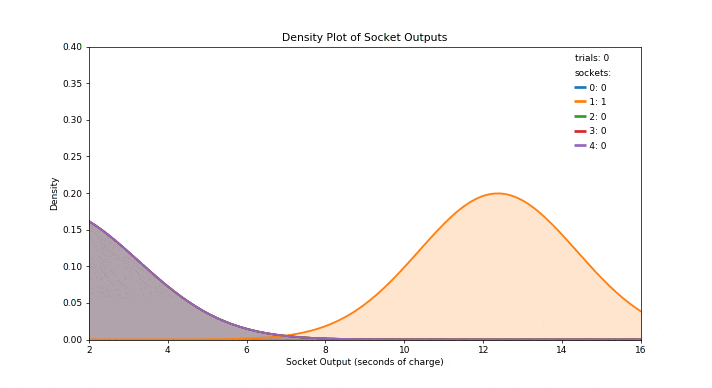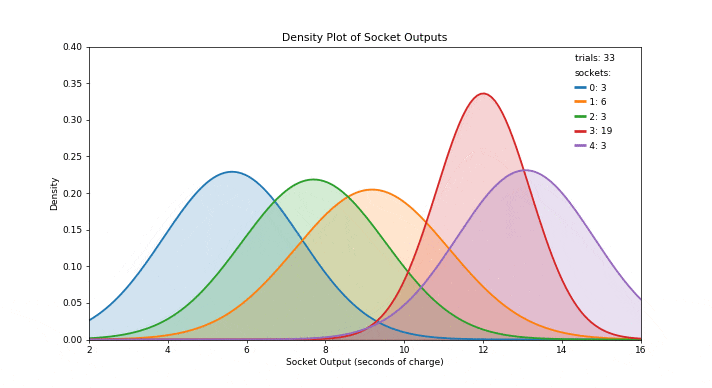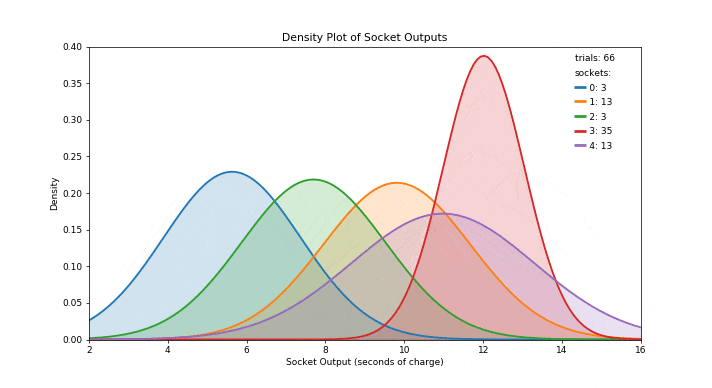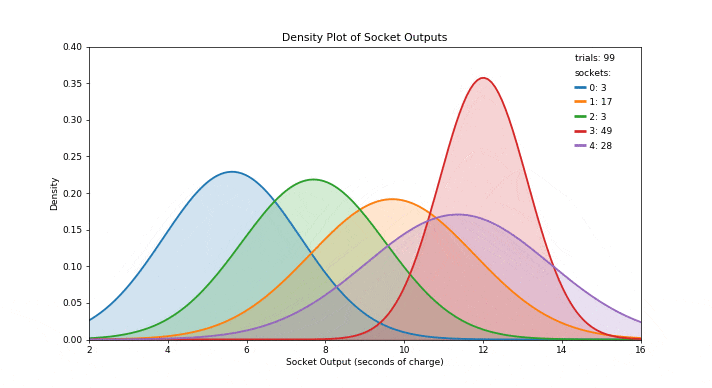
在从一组可能的行动中选择行动时,汤普森抽样采用了贝叶斯方法。在贝叶斯术语中,我们的初始估计被称为先验概率,当我们看到一些数据并改进这个估计后,我们形成了后验概率。当先验和后验都具有相同类型的概率分布时,它们被称为共轭分布。此外,当这种情况发生时,先验被称为似然分布的共轭先验(可以认为是数据的实际分布)。当似然概率分布具有更常见的分布之一时,其共轭先验的类型可以在维基百科上的共轭先验表中找到。此外,对于每种类型的共轭先验,此表指定了一组超参数,这些超参数可以在看到一些数据后进行更新,以从先验移动到后验。通过这种方式,概率模型变得更加准确,让我们对采取的最佳行动做出更明智的选择。汤普森抽样有几个优点,有助于其受欢迎程度:
- 探索和开发的平衡:它自然而然地平衡了对鲜为人知的机器的探索和对已知具有更高回报的机器的开发。
- 贝叶斯方法:它结合了先验知识,并以有原则的方式更新信念,使其对奖励分配的不确定性具有鲁棒性。
- 性能:与其他策略相比,它已被证明表现良好,尤其是在试验数量有限的情况下。
- 适应性:它可以轻松适应不断变化的环境,机器的奖励概率随时间变化。
- 简单性:尽管具有坚实的理论基础,但该算法易于实现。
汤普森抽样的过程包括:
- 初始假设:从一组关于各种股票潜在回报的信念开始。
- 决策:根据这些信念选择要投资的股票,对被认为具有更高回报的股票给予更多权重。
- 从结果中学习:根据从所选股票中观察到的实际回报更新信念。
- 迭代过程:重复此过程,随着时间的推移完善其策略,以最大化投资组合回报。
考虑一个场景,一个投资者正在评估三只股票。根据初始数据和汤普森抽样,投资者决定将更多资金分配给估计回报率最高的股票。随着市场条件的变化和新数据的出现,汤普森抽样重新计算概率,帮助投资者调整他们的投资组合,专注于最有前途的股票。下面是一个 Python 代码,它演示了用于选股的汤普森抽样,为简单起见,假设二元结果(利润/损失):
import numpy as np
stock_returns = {'Stock A': [0.05, 0.02, 0.05], 'Stock B': [0.1, -0.04, 0.08], 'Stock C': [0.03, 0.04, 0.02]}stocks = list(stock_returns.keys())def thompson_sampling(stock_returns, n_iterations=100): np.random.seed(42) for _ in range(n_iterations): sampled_returns = {} for stock, returns in stock_returns.items(): alpha = 1 + sum(np.array(returns) > 0) beta = 1 + sum(np.array(returns) < 0) sampled_returns[stock] = np.random.beta(alpha, beta) chosen_stock = max(sampled_returns, key=sampled_returns.get) print(f"Chosen stock for this iteration: {chosen_stock}")thompson_sampling(stock_returns)此代码有助于根据历史表现数据决定下一步要关注的股票。Thompson Sampling 提供数据驱动的股票交易方法,允许:
- 更好的风险管理:通过不断学习,它有助于识别和减轻潜在的损失。
- 动态投资组合调整:它支持基于性能的实时优化,而不仅仅是历史平均值。
- 探索与开发:它巧妙地在坚持已知的赢家和探索新机会之间进行权衡。
汤普森抽样提供了一种原则性的方法,以应对股市的不确定性。通过利用过去的业绩数据,投资者可以做出更明智的决策,从而有可能带来更好的投资结果。随着金融格局的发展,像汤普森抽样这样的工具在制定既动态又基于合理概率推理的策略方面变得非常宝贵。
本文内容仅仅是技术探讨和学习,并不构成任何投资建议。
Be First to Comment