图神经运算符 （GNO）能不能用于炒股？

作者：老余捞鱼

原创不易，转载请标明出处及原作者。

写在前面的话：在不断发展的机器学习和金融技术领域中，图神经运算符 （GNO） 已成为对复杂系统进行建模的强大工具。这篇博文将探讨什么是 GNO、它们的用途以及如何将它们应用于具有挑战性的股票价格预测任务。

一、图神经运算符及其用途

Graph Neural Operators 是 Graph Neural Networks （GNN） 的扩展，旨在学习和操作图形结构数据。传统的 GNN 使用固定的图形结构，而 GNO 可以处理动态图形并学习近似在图形上定义的函数空间之间映射的复杂运算符。

GNO 的主要目的是对实体 （节点） 具有复杂、相互依赖的关系 （边） 的系统中的行为进行建模和预测。它们在以下场景中表现出色：

1. 底层系统可以用图表示。
2 实体之间的关系对于预测非常重要
3 系统表现出非线性动力学

GNO 通过学习近似连续运算符来实现这一点，使他们能够捕获数据中复杂的模式和依赖关系。

二、使用 GNO 对股票价格预测进行建模

股票市场是具有相互依存实体的复杂系统的典型例子。每只股票都可以被视为图表中的一个节点，其边表示股票之间的关系或相关性。这些关系是动态的，可能会根据各种因素（如市场状况、公司绩效和全球事件）随着时间的推移而变化。

在我们的股票价格预测模型中，我们使用 GNO 来捕获这些复杂的关系并预测未来的股票价格。以下是我们解决问题的方法：

1. 数据表示：我们使用多家公司的历史股票价格作为我们的输入数据。每只股票都是我们图中的一个节点，边缘由股票价格之间的相关性决定。

2. 图形构建：我们根据历史价格走势计算相关矩阵，并使用它来在相关性高于特定阈值的股票之间创建边缘。

3. 特征工程：每个节点（股票）的特征是设定时间段内的历史价格数据。

4. 预测任务：我们的 GNO 模型旨在同时预测所有股票的第二天价格，同时考虑到它们之间的相互依赖关系。

2.1 架构和流程

我们的股票价格预测 GNO 模型遵循以下一般架构和流程：

1. 输入层：考虑图形结构（节点和边）和节点特征（历史价格）。

2. 图卷积层：在节点之间执行消息传递的多个层，允许信息通过图传播。

3. 全连接层：处理图形卷积的输出以做出最终预测。

4. 输出层：同时生成所有股票的预测。

通过模型的数据流如下所示：

1. 历史股票价格数据经过预处理和规范化。
2. 根据股票价格相关性构建图表。
3. 将图形和节点特征馈送到 GNO 模型中。
4. 模型执行多轮消息传递和特征转换。
5. 最后一层生成所有股票的预测。
6. 对预测进行非规范化以获得实际的股票价格预测。

2.2 代码说明

让我们分解一下我们实现的关键步骤：

数据准备：
我们首先使用 yfinance 库下载历史股票价格数据。然后使用 MinMaxScaler 对数据进行归一化，以确保所有特征都处于相同的比例上。

图形构建：
我们从标准化的价格数据中计算出一个相关矩阵，并使用它来在相关性高于某个阈值的股票之间创建边缘。这构成了我们的图形结构。

模型定义：
我们的 ImprovedGraphNeuralOperator 类定义了我们的 GNO 的架构。它由多个图形卷积层 （GCNConv） 和全连接层组成。我们还加入了 dropout 以进行正则化。

训练循环：
模型使用均方误差作为损失函数，使用 Adam 作为优化器进行训练。我们遍历多个 epoch，执行向前和向后传递以更新模型参数。

预测和评估：
训练后，我们使用模型对整个数据集进行预测。然后，对这些预测进行非规范化以获得实际的股票价格。我们计算每只股票的平均绝对误差 （MAE） 以评估模型的表现。

可视化：
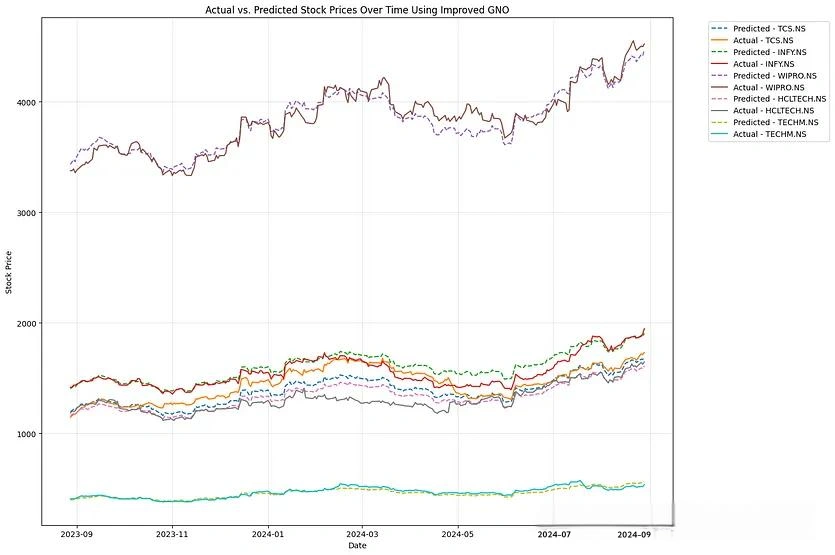
最后，我们创建一个图表，比较一段时间内的实际和预测股票价格，以便直观地检查模型的性能。

2.3 数据准备

让我们分解一下我们实现的关键组件：数据准备。
我们首先使用 yfinance 库下载历史股票价格数据。这为我们提供了一个 DataFrame，其中包含我们所选股票在一年内的收盘价。

data = yf.download（tickers， period='1y'， interval='1d'）['Close']data = data.dropna（） # 删除缺失值

接下来，我们使用 MinMaxScaler 对数据进行归一化。此步骤至关重要，因为它可以确保所有特征都处于相同的比例上，这有助于模型收敛和性能。

scaler = MinMaxScaler（）normalized_prices = scaler.fit_transform（data.values）

图形构建：
我们从标准化的价格数据中计算出一个相关矩阵。该矩阵根据价格变动表示不同股票之间的关系。

correlation_matrix = np.corrcoef（normalized_prices.T)

然后，我们使用此相关矩阵在相关性高于特定阈值的股票之间创建边。这构成了我们的图形结构。

edge_index = np.array（np.where（correlation_matrix > 0.5））edge_index= torch.tensor（edge_index， dtype=torch.long）

模型定义：
我们的 ImprovedGraphNeuralOperator 类定义了我们的 GNO 的架构。它由多个图形卷积层 （GCNConv） 和全连接层组成。我们还加入了 dropout 以进行正则化。

class ImprovedGraphNeuralOperator(nn.Module):  def __init__(self, input_dim, hidden_dim, output_dim):    super(ImprovedGraphNeuralOperator, self).__init__()    self.conv1 = GCNConv(input_dim, hidden_dim)    self.conv2 = GCNConv(hidden_dim, hidden_dim)    self.conv3 = GCNConv(hidden_dim, hidden_dim)    self.fc1 = nn.Linear(hidden_dim, hidden_dim)    self.fc2 = nn.Linear(hidden_dim, output_dim)    self.dropout = nn.Dropout(0.2)
  def forward(self, data):    x, edge_index = data.x, data.edge_index    x = F.relu(self.conv1(x, edge_index))    x = self.dropout(x)    x = F.relu(self.conv2(x, edge_index))    x = self.dropout(x)    x = F.relu(self.conv3(x, edge_index))    x = self.dropout(x)    x = F.relu(self.fc1(x))    x = self.fc2(x)    return x

这种架构允许通过图卷积层在节点（股票）之间传递消息，然后在完全连接的层中进行进一步处理。

训练循环：
我们使用均方误差作为损失函数，使用 Adam 作为优化器来训练模型。训练循环遍历多个 epoch，执行向前和向后传递以更新模型参数。

for epoch in range(epochs):  model.train()  optimizer.zero_grad()
  out = model(graph_data)  loss = criterion(out, graph_data.x)
  loss.backward()  optimizer.step()
  if (epoch + 1) % 50 == 0:  print(f’Epoch [{epoch+1}/{epochs}], Loss: {loss.item():.4f}’)

预测和评估：
训练后，我们使用模型对整个数据集进行预测。然后，对这些预测进行非规范化以获得实际的股票价格。

model.eval()with torch.no_grad():predicted_prices = model(graph_data).detach().numpy()
predicted_prices = predicted_prices.Tpredicted_prices = scaler.inverse_transform(predicted_prices)

我们计算每只股票的平均绝对误差 （MAE） 以评估模型的表现。

for i, ticker in enumerate(tickers):  mae = np.mean(np.abs(data.values[:, i] — predicted_prices[:, i]))  print(f”Mean Absolute Error for {ticker}: {mae:.2f}”)

可视化：
最后，我们创建一个图表，比较一段时间内的实际和预测股票价格。这允许对模型的性能进行目视检查。

plt.figure(figsize=(15, 10))for i, ticker in enumerate(tickers):plt.plot(data.index, predicted_prices[:, i], label=f’Predicted — {ticker}’, linestyle=’ — ‘)plt.plot(data.index, data.values[:, i], label=f’Actual — {ticker}’)
plt.xlabel(‘Date’)plt.ylabel(‘Stock Price’)plt.title(‘Actual vs. Predicted Stock Prices Over Time Using Improved GNO’)plt.legend(bbox_to_anchor=(1.05, 1), loc=’upper left’)plt.tight_layout()plt.grid(True, alpha=0.3)plt.show()

这种可视化有助于了解模型捕获股票价格随时间变化的趋势和模式的能力。

三、结论

Graph Neural Operators 提供了一种强大的方法来对股票市场等复杂系统进行建模。通过捕获股票之间的相互依赖关系，我们的 GNO 模型有可能做出比传统时间序列模型更明智的预测。

然而，重要的是要注意，股票价格预测是一项极具挑战性的任务，受许多因素的影响，其中许多因素是不可预测的。虽然我们的 GNO 模型提供了一种有趣的方法，但它应该与其他分析方法结合使用，而不仅仅是用于做出投资决策。与任何机器学习模型一样，持续优化、特征工程和严格的回溯测试对于提高实际应用程序的性能和可靠性至关重要。

本文内容仅仅是技术探讨和学习，并不构成任何投资建议。

转发请注明原作者和出处。