作者:老余捞鱼
原创不易,转载请标明出处及原作者。

写在前面的话:今天我想带领大家探索一种用于预测股票价格的稳健技术:对数域RANSAC线性回归。本文会详细阐述如何通过对数变换和RANSAC算法来提高预测的准确性和稳健性,特别是在处理非线性关系和正态化分布方面的优势。我们不仅会讨论理论,还会展示如何用Python实现这一模型预测AMZN股票价格。如果你对金融数据分析感兴趣,或者想了解如何将机器学习应用于投资领域,那么这篇文章绝对不应错过。
一、目标、挑战与方法
“Given a 10% chance of a 100 times payoff, you should take that bet every time.” — Jeff Bezos
“如果有10%的机会获得100倍的回报,你每次都应该下这个赌注”。- 杰夫-贝索斯
1.1 目标
我们的最终目标是开发出一些简单、稳健(尽管并不完全准确)且具有良好预测能力的时间序列预测(TSF)模型,帮助投资者从历史股票数据中解读模式,并利用它们形成较为可靠的数据驱动决策策略。
1.2 挑战
由于现实金融市场的不确定性,会让数据如过山车般起伏不定。那些突如其来的波动、令人措手不及的峰值,以及让人摸不着头脑的趋势转变,都让我们的老朋友——传统的时间序列分析(TSF)技术显得有些力不从心。在这个充满变数的金融舞台上,我们需要更强大的工具来洞察数据的真谛。
1.3 方法
在整个过程中,我们将测试和评估 Python 中的对数域 RANSAC 线性回归,以预测 AMZN 的历史价格。
要点 1:首先,我们强调对数线性回归在投资 TSF 中的巨大商业价值。
事实上,在 TSF 模型中对变量进行对数变换是处理非线性关系和将高度偏斜分布转化为更接近正态分布的一种非常常见的方法。
要点 2:其次,我们采用鲁棒共识算法 ,它可以只使用离群值来训练回归模型,同时检测并剔除离群值(分别与模型拟合良好或不拟合的数据点)。
具体来说,我们关注的是随机样本共识(RANSAC):这是一种迭代监督式 ML 算法,通过在训练过程中排除异常值,将线性回归算法提升到一个新的水平。
二、方法实现
2.1 数据准备
首先还是读取并绘制 AMZN 股票数据。
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import seaborn as sns
from matplotlib import pyplot as plt
df = pd.read_csv('AMZN_2006-01-01_to_2018-01-01.csv')
df.tail()
Date Open High Low Close Volume Name
3014 2017-12-22 1172.08 1174.62 1167.83 1168.36 1585054 AMZN
3015 2017-12-26 1168.36 1178.32 1160.55 1176.76 2005187 AMZN
3016 2017-12-27 1179.91 1187.29 1175.61 1182.26 1867208 AMZN
3017 2017-12-28 1189.00 1190.10 1184.38 1186.10 1841676 AMZN
3018 2017-12-29 1182.35 1184.00 1167.50 1169.47 2688391 AMZN
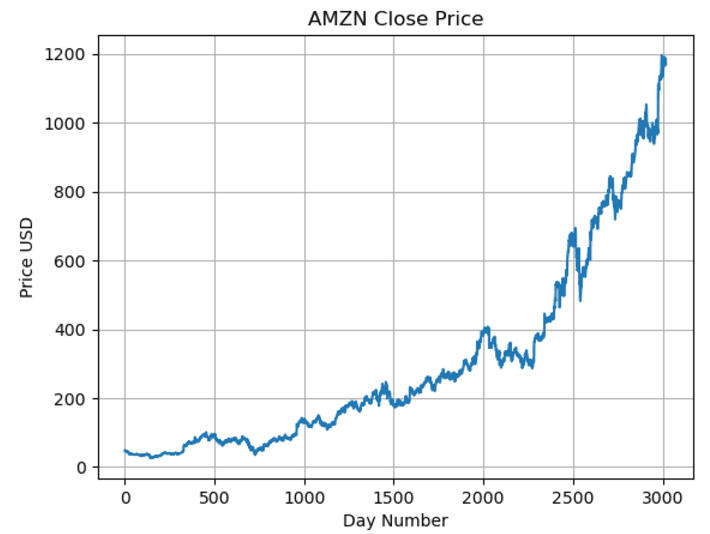
df['Close'].plot()
plt.title('AMZN Close Price')
plt.ylabel('Price USD')
plt.xlabel('Day Number')
plt.grid()
plt.show()下图是 AMZN 的收盘价。
接着进行数据准备和对数转换:
df1=df.reset_index(drop=False)
df2=df1.rename(columns={"index": "Days", "Close": "Price"}, errors="raise")
# Calculate the logarithm of the price and add it as a new column 'Log_Price'
df2['Log_Price'] = np.log10(df2['Price'])
# drop first 10 rows
df3=df2.iloc[10:, :]2.2 RANSAC 线性回归
实施 RANSAC 线性回归算法:
#The RANSAC Model
# Import relevant libraries and modules
from sklearn.linear_model import RANSACRegressor
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
# Instantiate the RANSAC Regressor with 'residual_threshold' = 0.1 and fit the model
ransacReg = RANSACRegressor(LinearRegression(), residual_threshold = 0.1, random_state = 0)
model4 = ransacReg.fit(df2[['Days']], df2['Log_Price'])
# Label the inliers and add them as a column in a new dataframe 'data_ransac'
inlier = ransacReg.inlier_mask_
data_ransac = df2.copy(deep=True)
data_ransac['Inlier_Ransac']= inlier
# Drop the outliers from the 'data_ransac' dataframe
data_ransac.drop(data_ransac[data_ransac['Inlier_Ransac'] == False].index, axis=0, inplace=True)
# Calculate the ratio of inliers after RANSAC regression
print('Ratio inliers vs total after RANSAC regression: ', len(data_ransac)/len(df2))
# Predict the model and calculate the R2 score
pred_model4 = ransacReg.predict(data_ransac[['Days']])
print ('R2 score after RANSAC regression: ', r2_score(data_ransac['Log_Price'], pred_model4))
Ratio inliers vs total after RANSAC regression: 0.7373302418019212
R2 score after RANSAC regression: 0.9866383665012699绘制去除 RANSAC 离群值后的 AMZN 历史价格数据图。
# Plot the data
plt.figure(figsize=(6,4))
plt.scatter(data_ransac['Days'],data_ransac['Log_Price'], color = 'k', s=1)
plt.xlabel('Days')
plt.ylabel('Log price')
plt.grid()
plt.title('Historical price data of AMZN after RANSAC');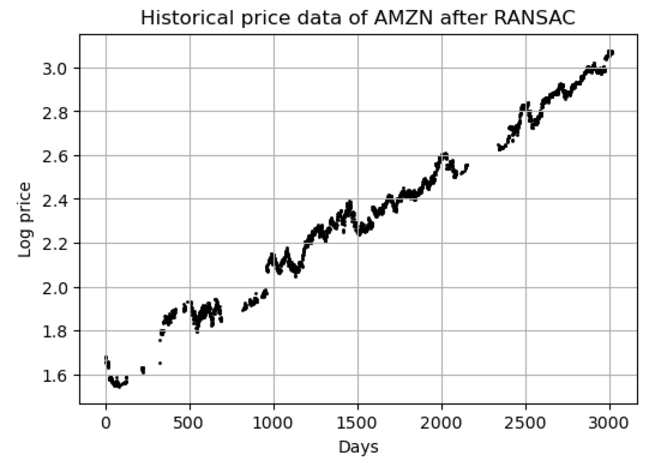
可以看到,在去除 RANSAC 异常值后的 AMZN 历史价格数据中,RANSAC 模型检测到了异常值并将其忽略。
接下来让我们将传统的 scikit-learn 线性回归应用于上述数据集。
# Import relevant libraries and modules
from sklearn import linear_model
from sklearn.model_selection import train_test_split
from sklearn import metrics
# Define X and y and split the data into 75% train and 25% test
X_ransac=data_ransac[['Days']]
y_ransac=data_ransac['Log_Price']
X_train_ransac,X_test_ransac,y_train_ransac,y_test_ransac = train_test_split(X_ransac,y_ransac,test_size = 0.25, random_state = 1)
# Instantiate the model and fit the training data
reg_ransac = linear_model.LinearRegression()
result_ransac = reg_ransac.fit(X_train_ransac,y_train_ransac)
# Calculate the coefficients and intercept
coefficients = reg_ransac.coef_
print(f'slope: {coefficients}')
interception = reg_ransac.intercept_
print(f'intercept: {interception}')
# Validate the model comparing the test data with the predicted data and calculate the R2 score
y_pred_ransac = reg_ransac.predict(X_test_ransac)
print('R2 score RANSAC Model:', metrics.r2_score(y_pred_ransac,y_test_ransac))
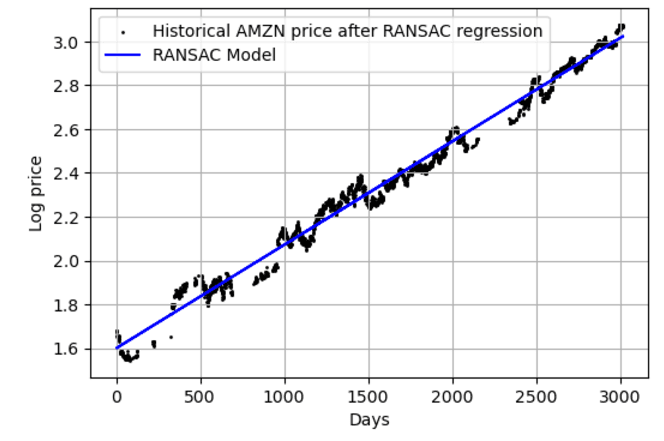
# Plot the model
plt.figure(figsize=(6,4))
plt.scatter(X_ransac,y_ransac, color = 'k', label='Historical AMZN price after RANSAC regression', s=1)
plt.plot(X_test_ransac,y_pred_ransac, color = 'b', label = 'RANSAC Model')
plt.xlabel('Days')
plt.ylabel('Log price')
plt.grid()
plt.legend();
slope: [0.00047224]
intercept: 1.5990502549514787
R2 score RANSAC Model: 0.9865737820332889下图是RANSAC 回归后的 AMZN 历史价格与 RANSAC 线性回归模型对比。
接着我们来制作反对数变换后的 AMZN 价格与 RANSAC 预测值对比图
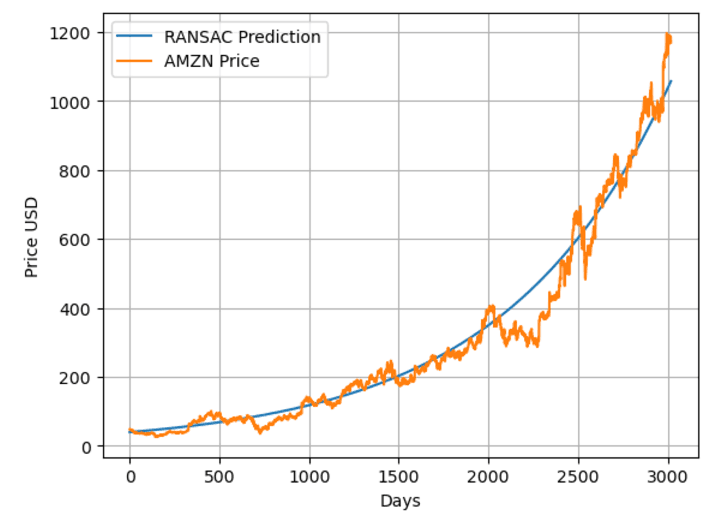
pred_ransac_model = ransacReg.predict(df2[['Days']])
df2['Hist_Pred_Log_Price_Ransac_Model']=pred_ransac_model
# Calculate back the predicted normal price.
df2['Hist_Pred_Price_Ransac_Model']=10**(df2['Hist_Pred_Log_Price_Ransac_Model'])
plt.plot(df2[['Days']],df2['Hist_Pred_Price_Ransac_Model'],label='RANSAC Prediction')
plt.plot(df2[['Days']],df2['Price'],label='AMZN Price')
plt.xlabel('Days')
plt.ylabel('Price USD')
plt.grid()
plt.legend();下图是反对数变换后的 AMZN 价格与 RANSAC 预测值对比。
三、对数转换的影响分析
我们可以通过实例化统计模型 OLS 回归 [1] 来评估对数变换 (LT) 的影响。
# Import relevant libraries and modules
import statsmodels.api as sm
from statsmodels.formula.api import ols在 LT 之前拟合 OLS 公式 ols_formula = ‘Price ~ Days’ (价格 ~ 天数)
ols_formula = 'Price ~ Days'
OLS = ols(formula = ols_formula, data = df2)
model = OLS.fit()
model_results = model.summary()
print(model_results)
OLS Regression Results
=============================================================================
Dep. Variable: Price R-squared: 0.795
Model: OLS Adj. R-squared: 0.794
Method: Least Squares F-statistic: 1.167e+04
Date: Mon, 25 Nov 2024 Prob (F-statistic): 0.00
Time: 12:17:38 Log-Likelihood: -18906.
No. Observations: 3019 AIC: 3.782e+04
Df Residuals: 3017 BIC: 3.783e+04
Df Model: 1
Covariance Type: nonrobust
=============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -132.6695 4.619 -28.722 0.000 -141.726 -123.613
Days 0.2863 0.003 108.014 0.000 0.281 0.292
=============================================================================
Omnibus: 346.632 Durbin-Watson: 0.003
Prob(Omnibus): 0.000 Jarque-Bera (JB): 478.601
Skew: 0.906 Prob(JB): 1.18e-104
Kurtosis: 3.723 Cond. No. 3.48e+03
=============================================================================在 LT 之后拟合 OLS 公式 ols_formula = “价格 ~ 天数
ols_formula2 = 'Log_Price ~ Days'
OLS2 = ols(formula = ols_formula2, data = df2)
model2 = OLS2.fit()
model_results2 = model2.summary()
print(model_results2)
OLS Regression Results
=============================================================================
Dep. Variable: Log_Price R-squared: 0.964
Model: OLS Adj. R-squared: 0.964
Method: Least Squares F-statistic: 8.141e+04
Date: Mon, 25 Nov 2024 Prob (F-statistic): 0.00
Time: 12:17:49 Log-Likelihood: 3284.7
No. Observations: 3019 AIC: -6565.
Df Residuals: 3017 BIC: -6553.
Df Model: 1
Covariance Type: nonrobust
=============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 1.5478 0.003 521.574 0.000 1.542 1.554
Days 0.0005 1.7e-06 285.316 0.000 0.000 0.000
=============================================================================
Omnibus: 109.395 Durbin-Watson: 0.018
Prob(Omnibus): 0.000 Jarque-Bera (JB): 136.849
Skew: -0.404 Prob(JB): 1.92e-30
Kurtosis: 3.659 Cond. No. 3.48e+03
=============================================================================推论:
- F-Statistic (after LT) / F-Statistic (before LT) ~ 7.3。这意味着 LT 后的 OLS 在统计意义上比 LT 前的 OLS 更显著。
- F-Statistic (before LT) / F-Statistic (after LT) | ~ 2.2。这意味着 LT 后的 OLS 残差比 LT 前的残差偏斜程度小两倍。
- 标准差误差(LT 前)/标准差误差(LT 后)~ 1540。标准偏差越小,说明我们的数据点越接近回归线,表明我们的模型拟合度越高。
- R2(LT 后)- R2(LT 前)~ 0.169。回想一下,R2(R 平方)表示因变量中可由自变量解释的方差比例。我们可以看到,LT 后的解释变异比例比 LT 前高 17%。
四、观点总结
在本文中,我们使用对数域 RANSAC 线性回归来预测 AMZN 的价格走势。首先,我们证明了 RANSAC 可以帮助识别和处理回归中的异常值。在处理有噪声的股票数据时,它是一种基础算法。
其次,我们已经证明,使用股票价格的对数而不是实际价格值是合适的。对数变换是一种方便的方法,可以将高度偏斜的变量转换为更加正常化的数据集。它用于从线性回归模型中得出更好的预测结果。
- 对数变换能够有效地将高度偏斜的股票价格数据转换为更接近正态分布的数据集,从而提高了线性回归模型的拟合度和预测准确性。
- RANSAC 算法是一种鲁棒的共识算法,它能够通过识别和排除异常值来提高模型的泛化能力,特别是在处理有噪声的金融时间序列数据时。
- 通过比较 LT 前后的 OLS 回归模型的 F-Statistic、STD Error 和 R2 值,本文证明了对数变换在改善模型统计性能方面的显著作用。
- 通过本文证明了 RANSAC 回归在这一领域中的应用潜力。而且在实际投资预测中使用多种机器学习方法的很重要。
谢您阅读到最后,希望本文能给您带来新的收获。祝您投资顺利!如果对文中的内容有任何疑问,请给我留言,必复。
本文内容仅限技术探讨和学习,不构成任何投资建议。
Be First to Comment