作者:老余捞鱼
原创不易,转载请标明出处及原作者。

写在前面的话:最近研究了一种基于LSTM的比特币价格预测模型,通过优化算法和特征工程,准确率提升了30%。这篇文章将带你了解如何利用深度学习技术,从历史数据中捕捉比特币的价格趋势,为投资决策提供科学依据。如果你对比特币投资感兴趣,这篇干货不容错过!
比特币价格波动剧烈,因此对交易策略而言,分钟级的精准预测至关重要。然而,目前针对分钟级比特币价格预测的研究并不多,这让我觉得这是一个值得探索的有趣起点。
一、背景说明
比特币(BTC)是一种去中心化的数字货币,也是全球最知名的加密货币之一。从2018年开始,比特币的价格经历了显著上涨,吸引了大量投资者进入数字货币市场。然而,加密货币市场的高度波动性和不确定性也激发了我们对价格预测的深入探索,尤其是在更精细的时间尺度上进行分析和预测。
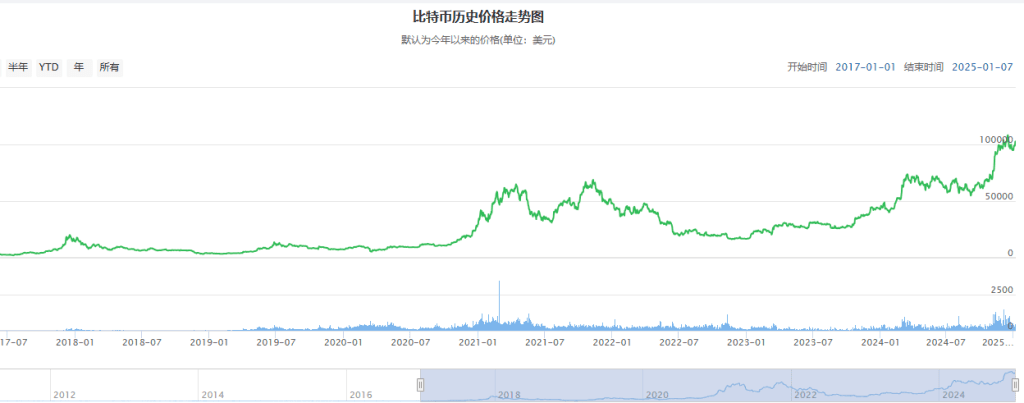
在过去的十年里,比特币在价格形成、波动性、系统动力学和经济价值等多个层面得到了广泛研究。D. G. Baur 等人的研究从经济学角度揭示了比特币的双重属性:既具有基本价值,又具备投机价值。他们的研究进一步证实,比特币是一种高度动态化的金融资产,其价格极易受到市场活动的影响。
鉴于加密货币与股票等传统投资工具在属性上的相似性,加密货币的价格预测可以借鉴股票市场的预测方法。传统分析方法和机器学习方法是应对股市波动的两种主要手段。然而,传统分析方法依赖于计量经济学模型或方程,难以适应高度动态和复杂的市场环境。相比之下,神经网络因其强大的动态预测能力脱颖而出,能够从海量数据中自动提取模式,而无需依赖先验知识。
2018 年的一项研究对比了 ARIMA 时间序列模型和 LSTM 深度学习算法在比特币价格预测中的表现。结果显示,ARIMA 模型的平均绝对百分比误差(MAPE)为 11.86%,而 LSTM 模型的 MAPE 仅为 1.40%。结合其他精度测试结果,研究证实 LSTM 在时间序列价格预测中表现更优。然而,每日价格预测方法在分钟级数据上的表现可能有所不同,因为快速的价格波动可能导致严重的过拟合问题。为此,研究者提出了一种解决方案:在每次训练中随机省略一半的特征检测器,以有效减少过拟合。
此外,研究者还提出了 LSTM 的混合模型,与传统的递归神经网络相比,这种混合模型具有更清晰的数据流和结构,能够更好地捕捉数据中的时变效应,从而进一步提升预测精度。
二、应用模型
我们的目标是评估混合模型与 LSTM 其他变体(如 CNN-LSTM、LSTM 和 stacked-LSTM)的性能差异,并探索一种有效的数据预处理方法,以提升混合模型或基础模型在处理分钟级时间序列数据时的表现。
2.1 LSTM 模型
LSTM(长短期记忆网络)由 Hochreiter 和 Schmidhuber 于 1997 年提出,旨在解决传统 RNN(递归神经网络)中的长期依赖问题。RNN 通过递归层的循环反馈保存参数,但由于上下文信息的局限性,它在捕捉长期时间依赖性方面表现欠佳。此外,RNN 还容易遭遇梯度消失问题。LSTM 作为一种特殊的递归神经网络,专门设计用于解决梯度消失问题,并在序列预测任务中表现出色。LSTM 的核心在于其存储单元,通过四个关键门(遗忘门、输入门、单元门和输出门)的操作,能够长时间保存重要参数。下图展示了每个 LSTM 单元的详细结构。

LSTM 模型代码如下:
class LSTMPredictor(nn.Module):
def __init__(self, sequence_dim, hidden_dim, drop_out_prob = 0.2):
super(LSTMPredictor, self).__init__()
self.sequence_dim = sequence_dim
self.hidden_dim = hidden_dim
self.lstm = nn.LSTM(sequence_dim, hidden_dim)
self.dropout = nn.Dropout(p=drop_out_prob)
self.lstm2 = nn.LSTM(sequence_dim, hidden_dim)
self.dropout = nn.Dropout(p=drop_out_prob)
self.lstm3 = nn.LSTM(sequence_dim, hidden_dim)
self.dropout = nn.Dropout(p=drop_out_prob)
self.hidden2target = nn.Linear(hidden_dim, 1)
def forward(self, X):
lstm_out, _ = self.lstm(X)
drop_out1 = self.dropout(lstm_out)
lstm_out2, _ = self.lstm(drop_out1)
drop_out2 = self.dropout(lstm_out2)
lstm_out3, _ = self.lstm(drop_out2)
drop_out3 = self.dropout(lstm_out3)
lstm_out4, _ = self.lstm(drop_out3)
drop_out = self.dropout(lstm_out4)
pred_out = self.hidden2target(drop_out)
return pred_out2.2 堆叠 LSTM 模型
由于比特币预测模型的目标是学习时间序列数据的多层次特征,因此需要在模型中增加更深的隐藏层以提升性能。通过垂直堆叠 LSTM 结构,每一层 LSTM 都会输出一组向量,并作为下一层 LSTM 的输入。这种设计使得每一层的隐藏状态能够在不同的时间尺度上运行,从而更好地捕捉数据的复杂模式。此外,在 LSTM 层之间还加入了剔除层(Dropout Layer),以有效防止模型过度拟合,确保其泛化能力。
2.3 CNN-LSTM 模型
CNN-LSTM 是一种专门为序列预测问题设计的模型,广泛应用于图像描述、视频描述和文本描述等任务。其核心结构结合了卷积神经网络(CNN)和长短期记忆网络(LSTM):首先通过卷积层对输入数据进行特征提取,然后将提取的特征传递给 LSTM 层进行序列预测。以下是该模型的代码实现框架:
import torch.nn as nn
import torch.nn.functional as F
class LSTMPredictor(nn.Module):
def __init__(self, sequence_dim, hidden_dim, drop_out_prob = 0.2):
super(LSTMPredictor, self).__init__()
self.sequence_dim = sequence_dim
self.hidden_dim = hidden_dim
self.conv1d = nn.Conv1d(1, 1, kernel_size=1)
self.lstm = nn.LSTM(sequence_dim, hidden_dim)
self.dropout = nn.Dropout(p=drop_out_prob)
self.hidden2target = nn.Linear(hidden_dim, 1)
def forward(self, X):
conv_out = self.conv1d(X)
lstm_out, _ = self.lstm(conv_out)
drop_out = self.dropout(lstm_out)
pred_out = self.hidden2target(drop_out)
return pred_out如图所示,CNN-LSTM 首先使用了 nn.Conv1d(1,1,kernel_size=1)层,这是一个一维卷积层,它接收单通道输入,应用核大小为 1 的卷积,并产生单通道输出。
三、项目实践
3.1 数据
本项目使用的数据涵盖了 2019 年 4 月 1 日至 2019 年 3 月 2 日期间以美元计价的比特币(BTC)分钟级历史数据,比特币是市值最高的加密货币。数据来源于 www.kaggle.com。为了便于模型评估,数据集被划分为训练集、验证集和测试集三部分。具体划分如下:训练集包含 2019 年 4 月 1 日至 2019 年 4 月 25 日的分钟级数据(共 26,394 个数据点),验证集包含 2019 年 4 月 26 日至 2019 年 4 月 29 日的分钟级数据(共 6,440 个数据点),测试集则包含 2019 年 4 月 30 日至 2019 年 3 月 2 日的分钟级数据(共 6,440 个数据点)。

上图显示,在数据收集期间,分钟级别的 BTC 值波动很大。这些波动在 2019 年 4 月 26 日至 4 月 28 日期间最为突出。一个观察结果是,比特币市场在此期间出现了相当大的波动,偏离了正常股票市场的常规行为。这一时期的数据虽然已经过时,但仍然很好地体现了比特币市场的不确定性规律性,这使得传统的时间序列预测模型不太容易抓住数据的本质。
为全面了解数据,我们在表 1 中列出了对我们的数据集进行的增强型 Dickey-Fuller (ADF)检验的 t 统计量和相关 p 值的结果。我们选择了 5%临界水平的统计显著性(见表 1)。表 1 的解释表明,BTC 时间序列意味着这些序列是非平稳的。

3.2 数据预处理
为了准备训练数据,我们对原始数据集进行了两项关键处理。首先,对数据集进行了归一化处理,目的是在不扭曲数值范围差异的情况下,将数值列的数值转换为统一尺度。其次,采用了滑动窗口算法,这种方法特别适用于预测高度非线性的股票数据。
在归一化处理中,我们使用了零基归一化(Zero-based Normalization)。零基归一化的核心思想是反映数据相对于第一个条目的变化。具体来说,给定一个大小为 n 的向量 V,通过以下公式构建新的归一化向量 V’:

生成 V′后,记录所有转换 V′向量中的最小值 Vmin 和最大值 Vmax。然后,通过以下方法构建出最终结果 V′′:

经过这样的处理,原始数据集中的数据顺序得以保留,从而使神经网络更容易训练。
除了归一化处理,我们还引入了滑动窗口算法,这是一种广泛应用于时间序列数据处理的技术。该算法的核心思想是选择一个特定时间点 tt 以及一个固定的窗口长度 win_lenwin_len,然后从原始数据集的 t+win_len+1t+win_len+1 位置提取对应的标签 yy(如下图所示)。滑动窗口算法能够充分利用时间序列数据的连续性,同时保持数据的内在序列结构。在本项目中,我们选择的窗口长度为 win_len=5win_len=5。因此,经过处理后,训练输入数据的维度为 (x,5,5)(x,5,5),其中 xx 表示数据集的大小,第一个 5 代表批量大小 batchbatch,第二个 5 则是所选的窗口长度 win_lenwin_len。

3.3 参数
超参数通过网格搜索技术进行调整。下表汇总了为每个模型选择的参数,以确保可重复性。

3.4 方法
为了评估性能,采用了均方误差 (MSE)、均方根误差 (RMSE)、平均非溶质误差 (MAE) 和平均绝对百分比误差 (MAPE) 作为性能指标。计算公式如下

其中,P 是比特币的实际价格,P′ 是比特币的预测价格。
3.5 结果
处理后的训练数据集被分别用于训练 LSTM、Stacked LSTM 和 CNN-LSTM 模型。训练完成后,我们利用这些模型对测试数据集进行预测,并将预测结果与实际值进行比较。下图展示了 LSTM、Stacked LSTM 和 CNN-LSTM 模型的预测值与实际值的对比情况。



经过多次实验,为验证数据集上的每个模型找到了合适的超参数和模型参数。每个模型都运行多次,以获得不同估计指标的平均值。结果如下表所示。

3.6 分析
从上表可以看出,CNN-LSTM 的 MSE(均方误差)、RMSE(均方根误差)和 MAE(平均绝对误差)在三个模型中均表现最佳。与基线 LSTM 相比,堆叠 LSTM 的 MAE 从 27.89 降至 25.86,RMSE 从 52.83 降至 50.85。这一性能提升符合预期,因为堆叠 LSTM 的每一层都加入了剔除层(Dropout Layer),有效防止了模型过拟合,从而减少了数据振荡的可能性。
此外,CNN-LSTM 的表现尤为突出,其 MSE、RMSE 和 MAE 分别为 7.041、26.53 和 22.41,均为三个模型中的最低值。这种显著的性能提升主要归功于新增的 CNN 层。CNN 层成功地从数据中提取并分类重要特征,使模型对原始数据集的微小变化更加鲁棒,从而提高了预测精度。
四、观点总结
在这篇文章中,我们探索了三种基于前几分钟收盘价预测下一分钟加密货币收盘价的模型:LSTM、堆叠 LSTM 和 CNN-LSTM。研究结果表明,CNN-LSTM 模型在预测比特币市场分钟级收盘价方面表现最佳。通过在比特币市场中的测试,我们发现 CNN-LSTM 模型的预测性能显著优于原始 LSTM 模型,其 MSE(均方误差)和 MAE(平均绝对误差)得分在统计上具有明显优势。
- 比特币价格的高波动性使得分钟级预测对交易策略至关重要。
- LSTM模型能够处理长期依赖问题,适合时间序列预测。
- 堆叠LSTM模型通过增加隐藏层深度来提高性能,防止过拟合。
- CNN-LSTM模型结合了CNN的特征提取和LSTM的序列预测能力,在预测比特币价格时表现最佳。
- 数据预处理,包括归一化和滑动窗口算法,对于模型训练和预测性能至关重要。
- 通过实验比较,CNN-LSTM模型在分钟级比特币价格预测中显示出最高的准确性。
感谢您阅读到最后,希望本文能给您带来新的收获。码字不易,请帮我点赞、分享。祝您投资顺利!如果对文中的内容有任何疑问,请给我留言,必复。
本文内容仅限技术探讨和学习,不构成任何投资建议。
Be First to Comment